Skip to main content

Stealth Address AA Plugin

TL;DR

The proposal is a privacy-preserving smart account utilizing stealth address.

I. Problem​

While Account Abstraction (AA) has been instrumental in providing flexible verification logic beyond the traditional ECDSA signature, there remains the need to confirm your identity and prove ownership of the wallet. Whether it’s a private key, an enclave-based key, or even biometric data, some form of identification is essential.

ECDSAValidator​

Within the ZeroDev Kernel’s ECDSA Validator, the owner’s address is stored on-chain. This approach serves the purpose of verifying the signature originating from the signer. However, this could compromise the privacy of smart accounts by making ownership information publicly accessible.

struct ECDSAValidatorStorage {
    address owner;
}

function validateUserOp(UserOperation calldata _userOp, bytes32 _userOpHash, uint256)
        external
        payable
        override
        returns (ValidationData validationData)
{
    address owner = ecdsaValidatorStorage[_userOp.sender].owner;
    bytes32 hash = ECDSA.toEthSignedMessageHash(_userOpHash);
    if (owner == ECDSA.recover(hash, _userOp.signature)) {
        return ValidationData.wrap(0);
    }
    if (owner != ECDSA.recover(_userOpHash, _userOp.signature)) {
        return SIG_VALIDATION_FAILED;
    }
}

II. Solution​

To mitigate this privacy concern, we employs the use of Stealth Addresses. These are designed to obfuscate the identity of smart account owners.

caption

Aggregate Signature​

However, the practical limitations of generating shared secrets and corresponding private keys within existing wallet UIs present a challenge. To overcome this, we propose using aggregate signatures that can be verified by the contract.

Aggregate ECDSA Signing​

Given private key of owner: privownerpriv_{owner} , shared secret key: privsharedpriv_{shared} (derived from ephemeral private key and user’s public key) and message: mm.

  1. Generate (r,s)(r, s) signature from signing mm using privownerpriv_{owner}.
  2. Calculate the aggregate signature s′=s(h+r∗privshared)s' = s(h + r ∗ priv_{shared} )
  3. The aggregate signature is (r,s′)(r, s')

Aggregate ECDSA Verifying​

The aggregate signature

s′=s(h+r∗privshared)=k−1(h+r∗privowber)(h+r∗privshared)=k−1(h2+ht∗(privowner+privshared)+r2∗privowner∗privshared)\begin{align} s' &= s(h+r*priv_{shared}) \\ & = k^{-1}(h + r*priv_{owber})(h + r*priv_{shared}) \\ & = k^{-1}\left(h^2+ht*\left(priv_{owner}+priv_{shared}\right)+r^2*priv_{owner}*priv_{shared}\right) \\ \end{align}

We notice that:

pubstealth=G∗(privowner+privshared)pub_{stealth} = G*(priv_{owner}+priv_{shared})
dhowner_shared=G∗(privowner∗privshared)dh_{owner\_shared} = G*(priv_{owner}*priv_{shared})

We can thus verify the aggregate signature by:

  1. Calculate the inverse of aggregate signature
s1=s′−1s_1 = s'^{-1}
  1. Calculate R′R^′ and take its x-coordinate r′=R′.xr^′ = R^′.x
R′=(h2∗s1)∗G+(h∗r∗s1)∗pubstealth+(r2∗s1)∗dhowner_sharedR^′ = ( h^2 ∗ s_1 ) ∗ G + ( h ∗ r ∗ s_1 ) ∗ pub_{stealth} + ( r^2 ∗ s_1 ) ∗ dh_{owner\_shared}
  1. The result is r==r′r == r^′

III. Stealth Smart Account​

StealthAddressValidator​

Within the framework of our validator, we’ll securely store the stealth address, stealth public key, and the Diffie-Hellman key. Importantly, to bolster user privacy, the owner’s address will not be stored in the validator. This design ensures that there is no explicit connection between the smart account and its respective owner.

struct StealthAddressValidatorStorage {
uint256 stealthPubkey;
uint256 dhkey;
address stealthAddress;
uint8 stealthPubkeyPrefix;
uint8 dhkeyPrefix;
}

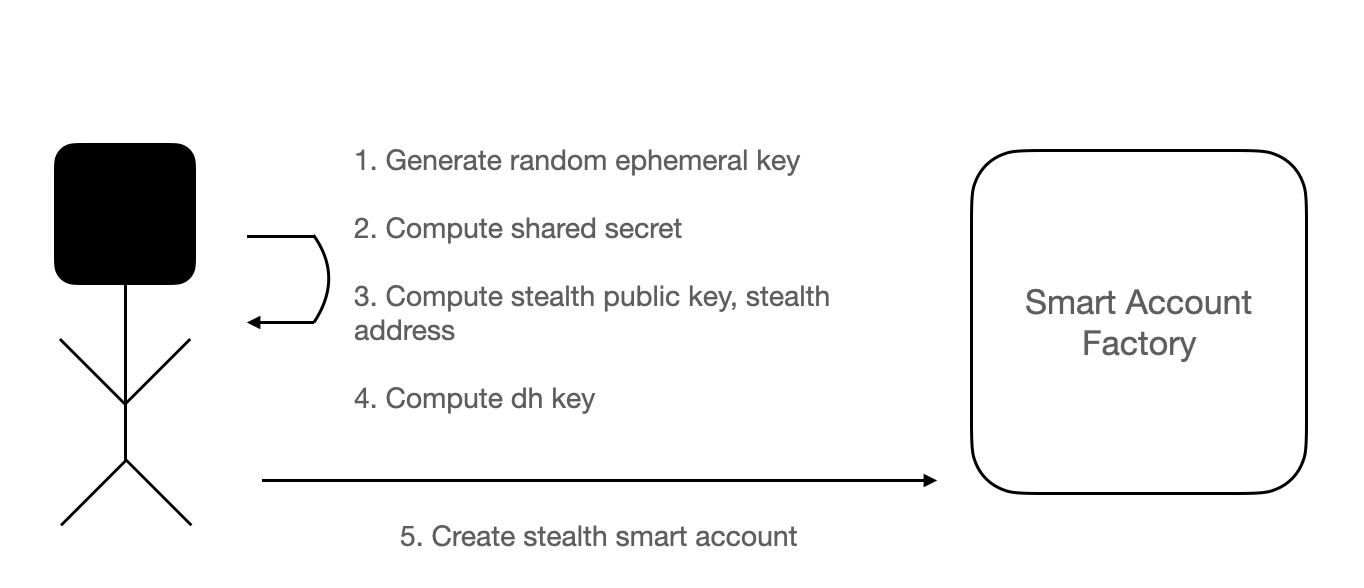
Workflow​

The following is the workflow of creating a stealth smart account:

caption

Further Improvement​

While our stealth smart accounts are self-created, eliminating the need for separate viewing and spending keys used in standard stealth address implementations, our aim is to ensure compatibility with ERC-5564. This will enable senders to transfer tokens to recipients while maintaining the recipient’s anonymity.